Una strana teoria geometrica del Tutto

 

La ragione che non è segreta:
una strana teoria geometrica del Tutto
Laura Corsi
AGC Edizioni – 2018

 

Scrive Giordano Bruno, nella sua opera “Il triplice minimo e la misura”: «Vi sono all’inizio tre archetipi, nella cui superficie è la regola di ogni numero, misura e figura. Assegno il primo ad Apollo, il secondo si adatta perfettamente a Minerva, il terzo è proprio di Venere, in quanto ognuno riconosce nel volto misterioso dell’archetipo il proprio sigillo e segreti». Il filosofo nolano era sul punto di intuire un misterioso schema nascosto e ricorrente delle cose della natura. Questa considerazione è il tema fondamentale della nuova ricerca di Laura Corsi, di recente pubblicazione, nel volume “La ragione che non è segreta – Una strana teoria geometrica del Tutto”, incentrata sulla qualità geometrica della natura, da cui emerge l’intimo parallelismo tra un simbolo e le leggi con cui la natura stessa si esprime e che richiama alla mente un concetto junghiano più volte ricordato anche da Marie Louise von Franz: gli archetipi sono espressioni delle categorie profonde della mente, così come il numero è espressione della struttura profonda della realtà.

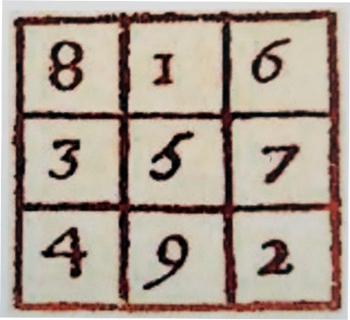
Il lavoro di ricerca di Laura Corsi si prefigge un interessante obiettivo: stimolare una riflessione sulle sconcertanti corrispondenze che emergono tra il regno astratto dei numeri e la realtà tangibile della natura. La base sostanziale di partenza di tutta la teoria svolta nel corso del volume, è rappresentata da un simbolo di origini lontanissime nella storia: la matrice matematica del Quadrato Magico. Si tratta di una griglia di numeri molto particolare con una storia di oltre quattro millenni, la cui proprietà singolare è la seguente: la somma dei numeri di ogni riga, colonna o diagonale produce sempre lo stesso risultato costante.

Questo simbolo è sempre stato presente in tutte le antiche culture della storia dell’uomo: nella Cina di oltre 4000 anni fa, nella Mesopotamia del XX secolo a.C., nell’Eliopolis delle prime dinastie egizie, passando successivamente per i Pitagorici, gli alchimisti e personalità di rilievo dell’Umanesimo e del Rinascimento toscano. Il quadrato magico è, infatti, un oggetto matematico che rientra nelle remote simbologie archetipiche di ispirazione mistico-filosofico e non deve trarre in inganno l’aggettivo “magico” (il quale, ai giorni nostri, ha erroneamente assunto un significato ingannevole e superstizioso) in quanto le sue origini risalgono alla Scienza dei Magi dei grandi sapienti d’Oriente e degli antichi scienziati, da sempre attenti ai ritmi del tempo, della natura e dell’intimo sconosciuto dell’uomo.

Nel caso specifico, l’autrice considera il quadrato di dimensioni 3×3 e, riflettendo sulle sue proprietà, si domanda: “se la Natura nasconde, o meglio, rivela le sue leggi con il numero, può un sistema di numeri al tempo stesso così semplice e straordinario, raccontare di una legge del mondo naturale? Può questo stupefacente strumento matematico, questa perfetta architettura di cifre contenuta nel quadrato essere lo specchio aritmetico di una realtà tangibile?” (p.6)

Ciò che suscita l’immediato interesse e curiosità del lettore è la scelta del metodo utilizzato da Laura Corsi nel corso di questa esplorazione. Sulle parole di Cristoforo Colombo “non si può mai attraversare l’oceano se non si ha il coraggio di perdere di vista la riva”, l’autrice si addentra con coraggio in zone d’ombra non convenzionali, affrontando le anomalie come indicatori delle regole stesse. In altri termini, viene abbandonato il conformismo del metodo scientifico, ritenendo che è proprio nella rottura della logica consolidata che si apre la strada alla scoperta. Vengono così in mente le parole di Paul Feyerabend, il noto filosofo della scienza, che nel suo trattato “Contro il metodo” ci ricorda che: “data una qualsiasi regola, per quanto “fondamentale” o “necessaria” per la scienza, esistono sempre circostanze in cui è consigliabile non solo di ignorare la regola stessa, ma di adottare il suo opposto“.

In altre parole, abbandonare il pregiudizio per l’autrice significa “analizzare il dato con rigore formale, cercando il sostegno della logica e della matematica ma significa anche assecondare l’intuizione e l’empatia con l’oggetto di studio”. (p.16)

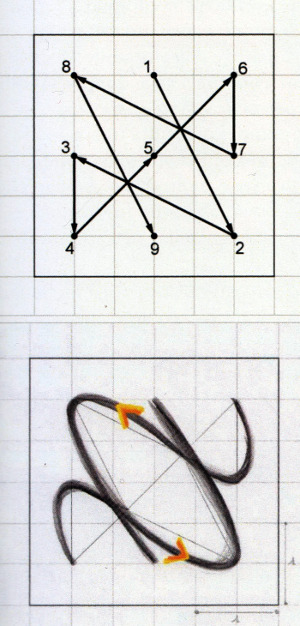
Il percorso di Laura Corsi parte quindi da un’interessante traslazione del quadrato magico da matrice matematica a figura geometrica, per rilevare subito che quest’ultima rappresenta due spirali intrecciate, in analogia con la catena del DNA umano e la forma delle galassie a spirale. Tuttavia, si tratta solo di una prima semplice intuizione che aprirà la strada, nel corso della ricerca, alle porte della fisica quantistica, della meccanica relativistica, della matematica dei frattali, della fisica nucleare e così via verso inaspettate frontiere.

Immediatamente appare una stretta relazione tra il quadrato e i tre numeri “magici” della matematica: π (costante di Archimede), φ (sezione aurea) e √2 (costante di Pitagora). Tre numeri irrazionali, la cui lunghezza si estende all’infinito senza schemi ripetitivi ma che rappresentano le fondamenta architetturali della natura e dell’Universo.

Immagino che queste prime “coincidenze significative” abbiano fornito all’autrice il necessario stimolo per approfondire questa singolare rappresentazione geometrica. Una sorta di luce verde all’ingresso di una galleria oscura nella quale, man mano che si procede, piccoli fari a terra si illuminano per indicare il percorso in corrispondenza di ciascuna nuova rivelazione. Con questi presupposti Laura Corsi si avventura nel viaggio verso la fisica quantistica snocciolando ciascuna meta come i grani di un rosario, come perle di una collana sorretta dal filo della sua ricerca.

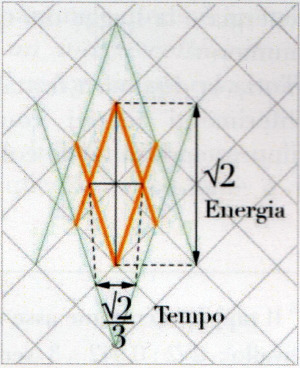
Scopre così che la sua geometria, apparentemente semplice e legata a un simbolo millenario, è in grado di instaurare un dialogo univoco non solo con le tre costanti matematiche citate in precedenza, ma anche con le costanti più celebri della fisica. Le due curve intrecciate, o meglio i due triangoli isosceli sovrapposti, contengono, infatti, relazioni di corrispondenza che coincidono con la costante di Planck, la velocità della luce, la costante di struttura fine, il modello atomico di Bohr e così via, fino a caratterizzare la dualità onda/particella della materia. In particolare, i due formidabili traguardi della scienza del ‘900 raggiunti da Albert Einstein e Max Planck (l’equivalenza di massa ed energia e la legge dei quanti), si specchiano nelle geometrie e nelle grandezze di questa incredibile griglia di numeri.

Interpretare il quadrato magico come un gruppo di simmetria – o meglio – come un sistema di vettori che concorrono a descrivere un campo vettoriale chiuso nella definizione del quadrato stesso, le consente così di attraversare in sicurezza tutte le principali leggi della fisica moderna, fornendo una descrizione alternativa dei fenomeni infinitesimali attraverso una semplice visione geometrica. L’intuizione di Laura Corsi ricorda, seppur applicata a un campo molto più vasto, quella avuta da Richard Feynman quando descrisse la teoria quantistica dei campi secondo il suo modello “a diagrammi”.

Tuttavia non si tratta solo di una nuova rappresentazione. C’è qualcosa di molto più ambizioso e interessante nella ricerca della Corsi: gettare ancora uno sguardo al dibattito generato dalla “interpretazione di Copenaghen”, secondo cui le affermazioni probabilistiche della meccanica quantistica sono irriducibili. L’autrice, infatti, si chiede: “Veramente la probabilità è l’ultima frontiera oppure esiste la possibilità di conciliare gli opposti, alla luce del dinamismo della natura?” (p.51)

Dopo aver efficacemente analizzato tutte le corrispondenze della sua teoria con la fisica quantistica, Laura Corsi procede con coraggio anche nell’ambito della fisica nucleare, scoprendo come il suo nuovo modello geometrico si adatti – lasciando talvolta addirittura emergere soluzioni – anche alla fisica nucleare, al Modello Standard e ai decadimenti radioattivi. L’autrice, infatti, intravede e ipotizza nell’ambito della sua rappresentazione una sottostruttura interna all’atomo con identità specifica: il suo nucleo. A questo punto però le deduzioni si fanno ancora più interessanti quando nella prospettiva offerta si denota che il nucleo condivide con l’atomo a cui appartiene una prerogativa sostanziale ovvero il principio della doppia natura di onda e particella. Scrive la Corsi: «Ciò significa che la natura ondulatoria della materia può essere estesa anche nelle profondità del nucleo, dove peraltro traccia una struttura più articolata: proprio la fitta trama ondulatoria dà conto delle potenti forze di legame che agiscono all’interno del nucleo e in particolare della forza forte» (p. 165)

Se davvero però la ricerca condotta deve rappresentare “una strana teoria geometrica del Tutto”, non può essere disattesa la sua analisi e applicazione negli ambiti dello spaziotempo e delle forze fondamentali. Analizzando la struttura geometrica della matrice e traslando i risultati raggiunti nell’analisi quantistica, l’autrice arriva a dimostrare la coerenza del modello geometrico ipotizzato con un’ordinata trama composta di collegamenti, che altro non sono che le linee di forza del campo gravitazionale. Sorprende a questo punto l’analogia con una delle più giovani teorie dello spaziotempo: la Gravità Quantistica a Loop (LQG) di cui uno dei maggiori esponenti è il fisico italiano Carlo Rovelli. Si tratta di una teoria matematicamente molto complessa ma dalle conclusioni sorprendenti: l’Universo non è uno spazio continuo ma è formato da grani, cioè da minuscoli “atomi di spazio” che formano una rete di relazioni che tesse la trama dello spazio stesso. Ma è la seconda conseguenza della teoria a essere la più estrema. Scrive Rovelli: «Come sparisce l’idea dello spazio continuo che contiene le cose, così sparisce anche l’idea di un tempo elementare e primitivo che scorre indipendentemente dalle cose. Le equazioni che descrivono grani di spazio e materia non contengono più la variabile tempo».

Lo spaziotempo descritto da Laura Corsi attraverso la matrice è uno spaziotempo su scala infinitesimale quantistica eppure, nonostante ciò, sembra comportarsi secondo le regole previste dalla teoria della relatività per la scala macroscopica. Si è dunque veramente giunti alla definizione di una teoria unificatrice – ricercata da decenni di studi scientifici – in grado di rendere compatibili i risultati quantistici con quelli relativistici? Come far dialogare uno spazio euclideo (a due dimensioni) con uno spazio non euclideo (curvo)? L’inaspettata risposta di Laura Corsi è nel linguaggio della geometria frattale, il solo capace di spezzare il rigore euclideo convergendo verso la logica con cui la natura esprime se stessa, in cui ogni parte è in risonanza con il tutto. “Tra l’infinitamente grande e l’infinitamente piccolo c’è solo l’infinitamente ripetuto” (p. 254)

Dalla prima all’ultima pagina di questa interessante ricerca esiste una logica ferrea che non può produrre per puro caso grandezze così significative per le logiche matematiche e di Natura. Il testo si sofferma particolarmente sulle inaspettate convergenze tra leggi geometriche e leggi della fisica, delineando così una teoria unificatrice comune a tutte le specifiche discipline della scienza moderna. Eppure appare anche evidente cogliere il significato unitario di quel “ponte tra psiche e materia”, più volte percorso da Wolfgang Pauli, che lo portò a scrivere, nella sua opera “Psiche e Natura”: «Come ho già ricordato in altra sede, la complementarità in fisica presenta una profonda analogia con i concetti di «coscienza» e «inconscio» in psicologia, in quanto ogni «osservazione» di contenuti inconsci comporta una ripercussione essenzialmente indeterminabile della coscienza su questi stessi contenuti. […] Il punto di vista definitivo deve far intravedere, tramite l’inconscio dell’uomo moderno, una linea di sviluppo verso una futura descrizione della natura che comprenda unitariamente physis e psiche. Per raggiungere una tale descrizione unitaria della natura, sembra necessario in primo luogo risalire al retroterra archetipico dei concetti scientifici».

Proprio nel suo intenso scambio epistolare con Pauli, Carl G. Jung rivelò qualcosa di molto più che una semplice analogia tra quanto si può osservare nelle dimensioni profonde della psiche e in quelle infinitesimali della materia, e in tal senso la ricerca di Laura Corsi tende allo stesso fine. D’altronde, così come, nell’ambito della Teoria del Campo Quantistico (QFT) la materia si manifesta in risposta alle intrinseche interazioni del campo, nella simbologia della psiche l’immagine si manifesta in risposta alle intrinseche interazioni dell’archetipo.

In altri termini, si ripropone il concetto ermetico di uomo come microcosmo nel macrocosmo, evidenziato anche dal fisico Richard Feynman nella sua poesia letta in occasione di un discorso alla National Academy of Science: « […]Di fronte al mare, stupito dallo stupore: io, un universo di atomi, un atomo nell’universo».